Откуда возникает мощь вычислительной машины
[прим.авт.: Главы 2 и 3 имеют технический характер. Читатель, чувствующий себя неуверенно, встречаясь с техническим материалом, может либо бегло просмотреть эти главы, либо отложить знакомство с ними до тех пор, пока он не прочтет остальную часть книги.]
Если бы мы увидели нечто чрезвычайно странное, скажем, облако с отчетливо правильными очертаниями, то нам бы захотелось выяснить, что это такое. И если бы нам сказали, что это некая "фуба", то мы бы спросили, что такое "фуба". Существуют, однако, повсюду вокруг нас вещи, которые являются столь неотъемлемой частью нашей жизни, что они не кажутся странными и мы не спрашиваем, что это такое. Так обстоит дело с машинами. Слово "машина" ассоциируется со сложным и в то же время в какой-то степени регулярным движением. Возвратно-поступательное движение иглы швейной машины так похоже на энергичную работу вращающихся толкающих шатунов, приводящих в движение колеса локомотива, и в то же время на тремор пульсирующего спускового механизма самых изящных часов, что подобные образы в достаточной степени дают представление о "машине". В достаточной для того, чтобы у нас больше не было необходимости спрашивать, что такое машина. Итак, машина - это регулярность, сложность, движение, мощь. Однако существует нечто кроме этого, и мы это знаем.
Мы включаем листоштамповочный пресс, и он кромсает руку рабочего, оказавшегося слишком близко. Именно регулярность машины является ее наиболее грозным свойством. Мы даем ей задание, и она, можно быть уверенным, выполняет его правильно, но слепо. Фраза "правосудие слепо" подразумевает, что оно действует почти (как машина, выполняющая свои функции, не обращая внимания на факты, не относящиеся к делу, но представляющие собой тем не менее факты. Для слепого правосудия не имеет значения, богат подсудимый или беден, мужчина он или женщина. Листоштамповочному прессу безразлично, какой материал в его зажимном устройстве - кусок металла или рука рабочего.
Подобно любой машине слепое правосудие и листоштамповочный пресс выполняют только то, для чего они предназначены, и выполняют они это точно.
Правильно работающие машины - не просто послушны закону - они олицетворение закона. Говорить, что определенная машина "работает правильно", значит утверждать, что она представляет собой воплощение некоторого закона, который мы знаем и хотим применить. Мы полагаем, например, что обычная настольная счетная машина служит олицетворением всем известных законов арифметики. Даже если она выдает неверные результаты, наша уверенность в "законности" машины столь сильна, что обычно мы предполагаем ошибку при перфорации данных. Лишь в случае повторных неправильных результатов мы решаем, что "с машиной что-то не так". Мы никогда не допускаем, что арифметические законы отменяются ии изменяются. В равной степени мы никогда не допускаем, что поведение машины своенравно, т. е. не послушно закону. Наоборот, чтобы восстановить ее правильное функционирование, мы пытаемся понять, почему машина ведет себя именно так, как она это делает сейчас, т. е. олицетворением какого именно закона в данном случае она является. Мы бываем удовлетворены, обнаружив, скажем, сломанную шестерню, вызвавшую аномальное поведение машины, и устанавливаем таким образом соответствующий закон машины. Теперь мы понимаем машину, с которой имеем дело, и, следовательно, в состоянии восстановить ее, т. е. преобразовать в ту машину, с которой мы имели дело с самого начала, - олицетворение обычных законов арифметики. В самом деле, часто мы очень огорчаемся, когда получаем машину из ремонта со словами: "Я не знаю, что с ней было. Я просто встряхнул ее и теперь она прекрасно работает". Это признание того, что не понят закон, определяющий поведение сломанной машины, и мы приходим к выводу, что теперь никто не в состоянии выяснить закон, определяющий поведение "отремонтированной" машины. Если мы пользуемся этой машиной, то становимся исполнителями какого-то закона, знать который нам не дано, т.
Одной из его деталей является штанга толкателя - стержень из нелегированной стали, нижняя часть которого насажена на распределительный вал, а верхняя может поднимать выпускной клапан соответствующего цилиндра. Когда в двигателе поворачивается коленчатый вал, то поворачивается также и распределительный вал с кулачками, сочлененными со штангами толкателя. В результате штанга толкателя движется вверх-вниз и точно в необходимый момент открывает и закрывает выпускной клапан цилиндра. В простейших бензиновых двигателях штанга толкателя обеспечивает и энергию, необходимую для перемещения клапана, и соответствующую синхронизацию. В более сложных двигателях, однако, она действует исключительно как устройство, подающее сигнал какому-нибудь другому механизму, уже непосредственно оперирующему клапаном. Можно допустить, что вместо него используется провод, присоединенный одним концом к устройству, определяющему момент, когда газы должны быть вытеснены из цилиндра, и другим - к электродвигателю, сообщающему соответствующее движение клапану. Многие современные автомобильные двигатели оснащены электронными системами впрыскивания горючего, действие которых очень похоже на описанное.
Существует определенный предел числа механических связей в автомобильном двигателе, допускающих замену устройствами передачи информации. В конце концов, двигатель должен передавать механическую энергию на колеса автомобиля. Это условие налагает на конструктора двигателя жесткие ограничения. Инженер вполне может предложить такую внутренне непротиворечивую совокупность законов, другими словами, конструкцию для двигателя, которую тем не менее реализовать было бы невозможно. Такая конструкция могла бы потребовать механической обработки металлов с допусками, например, которые просто нельзя обеспечить современными методами. Могло бы быть и так, что прочности материалов, необходимые для таких двигателей, нельзя было бы получить с помощью современных технологий. Много важнее, однако, что предложенная конструкция может оказаться принципиально нереализуемой из-за нарушений законов физики.
Именно по этой причине терпят неудачу все попытки создавать вечные двигатели. Законы, олицетворяемые некоторой машиной, действующей в реальном мире, должны в силу необходимости являться некоторым подмножеством законов, которым этот мир подчиняется.
Несомненно, абсурдно говорить о реализованной машине, т. е. машине, получившей материальное воплощение, которая не вступала бы во взаимодействие с реальным миром. Если бы она существовала, нам не дано было бы узнать об этом, поскольку для того, чтобы представить свидетельство своего существования, она должна была бы воздействовать на наши чувства, т. е. вступить в контакт с реальным миром. Во всяком случае, подобную машину нельзя было бы использовать, так как разве не понимаем мы "использование" как взаимодействие с внешним миром?
Существуют, однако, обстоятельства, при которых имеет смысл говорить о таких аспектах реальных машин, которые не связаны с их материальными воплощениями. Иногда приходится, например, обсуждать, что некоторая машина либо какая-то часть какой-либо машины должна делать совершенно независимо от того, каким образом или из каких материалов можно было бы создать механизм, реально выполняющий требуемые действия. Например, какой-то элемент бензинового двигателя должен определять, когда следует открывать и закрывать выпускной клапан цилиндра. Эту функцию может выполнять жесткая штанга толкателя или, как я отмечал, провод, соединенный соответствующим образом с датчиком и электродвигателем. Правило, на основе которого подобное устройство должно работать, закон, олицетворением которого оно должно являться, представляет собой некий отвлеченный принцип. Он не зависит от материала и физической реализации, короче говоря, ни от чего, за исключением мысли и здравого смысла. На основе такого правила или, как любят говорить инженеры, "функциональной спецификации" можно получить любое число конструкций, например, одна из них может быть механической, а другая - электрической "штангой толкателя".
Конструкция некоторой машины - это снова некая абстракция. Хорошую конструкцию, скажем, швейной машины можно передать нескольким изготовителям, каждый из которых будет выпускать швейные машины, совершенно не отличимые друг от друга. В таком случае подобная хорошая конструкция в каком-то смысле есть некоторая абстрактная швейная машина. Это машина, которая может производиться, - минус, так сказать, физические компоненты, комплектующее оборудование реальной швейной машины. Конструкция не зависит также и от носителя, на котором она может быть зафиксирована. Синьки чертежей машины не есть ее конструкция. В противном случае конструкция менялась бы при увеличении масштаба чертежа или при выполнении ело в другом цвете. Конструкция - это некоторая абстрактная идея так же, как и функциональная спецификация. Идеи же (скажем, идея машины, совершающей вечное движение) не связаны законами физики [Прим. ред.: По-видимому, трудно назвать идеей мысль, высказывание, предложение, противоречащее законам физики].
Писатели-фантасты беспрестанно выступают, в сущности, с функциональными спецификациями машин, которые могут оказаться физически нереализуемыми, так как нарушают незыблемые физические принципы. Одна из идей, которая появляется снова и снова, - это мгновенная связь через безбрежные пространства. Из физики же известно, что любое послание в какой бы то ни было форме не может быть передано из одного места в другое со скоростью, превышающей скорость света. Поскольку скорость света конечна (она равна приблизительно 300000 км/с), невозможна мгновенная связь даже на небольших расстояниях, по крайней мере с точки зрения современной физики. Бесполезны ли подобные идеи, предлагаемые научными фантастами? Нет. Потому что, хотя тела наши должны функционировать в мире, подчиняющемся естественным законам, наш разум может от него отрешаться. Мы можем перенести игру нашего воображения в мир, устроенный таким образом, что конечность скорости света, например, вообще не являлась бы ограничением для скорости связи.
Это означает не более того, что мы можем участвовать в играх, правила которых создаем сами. Мы можем определять степень соответствия (если оно вообще имеется) правил наших игр любым законам, которым, как мы считаем, подчиняется реальный мир. Игра "Монополия" [Прим. перев.: "Монополия" - настольная игра (типа нашей "вверх - вниз"), очень популярная в западных странах. В ней в условной форме воспроизводятся законы капиталистической экономики: в процессе игры можно продавать и покупать акции, приобретать и терять недвижимость, становиться миллионером и разоряться и так далее. Выигрывает тот, кому в процессе игры удается накопить наибольший "капитал" - фишки, в начале игры равномерно распределенные между ее участниками] могла бы существовать даже в тех мирах, если бы таковые существовали, где алчность не является реальностью.
Критическим свойством системы правил любой игры является полнота и логическая непротиворечивость. Они должны быть полными в том смысле, что для любого предложения о действии в процессе игры они позволяют определить, является оно допустимым или нет. Они должны быть логически непротиворечивы в том смысле, что не существует такого подмножества правил, которое определит допустимость некоторого действия, и одновременно некоторого другого подмножества, определяющего то же самое действие как недопустимое [прим.авт.: Существует множество игр, для которых не были доказаны либо логическая непротиворечивость, либо полнота правил в указанном здесь смысле. Когда в процессе подобных игр в связи с противоречивостью и неполнотой правил возникают затруднения, они обычно разрешаются усовершенствованием действующих правил. По прошествии некоторого времени усовершенствованная указанным образом совокупность правил рассматривается уже как "классическая". (Это наблюдение я позаимствовал у Оливера Селфриджа)]. Совершенно абстрактной игрой является такая, правила которой предусматривают отсутствие контакта с реальным миром, т.
е. игра, реализовать которую можно с помощью одного лишь разума. Шахматы, в которые играют на турнирах, не относятся к та.кой категории игр, поскольку их правила ограничивают время, которое шахматист может затратить на обдумывание своих ходов. Этот временный элемент определяет контакт шахмат с реальным миром и тем самым нарушает чистоту их абстрактности. Если же не учитывать это условие, то шахматы - абсолютно абстрактная игра [Прим. ред.: Это утверждение автора более чем спорно. Фактор времени всегда присущ игре в шахматы и в очных и в заочных соревнованиях. Кроме того, в шахматы играют люди (или машины), знания которых (или степень совершенства шахматных программ) практически полностью определяются реальным миром].
Другой путь сформулировать условие, предусматривающее полноту и логическую непротиворечивость правил игры в указанном смысле, - это потребовать, чтобы любые два арбитра, столкнувшись с одной и той же игровой ситуацией, не смогли не прийти к согласованному суждению. На самом деле "суждение" - неудачный термин, поскольку их решение будет получено в результате использования одной лишь логики. Это, по существу, не что иное, как детерминированный расчет, логический процесс с единственным возможным результатом.
Существует только одна разновидность вопросов, которые имеет смысл ставить арбитру чисто абстрактной игры. Участник игры может описать игровую ситуацию, скажем, расположение фигур на шахматной доске до осуществления рассматриваемого действия и после того, как оно реализовано. Его вопрос должен состоять в том, возможно или невозможно перейти из исходного расположения во второе за один "ход". Участник игры мог бы, например, сказать: "Я объявил шах, а он сделал рокировку. Имеет ли он право так играть?" Или: "Я пошел в пики, а он побил мою карту червами, хотя у него были пики на руках. Имеет ли он право так играть?" Допустимость только подобных вопросов объясняется тем, что правила абстрактной игры определяют лишь, какие игровые ситуации могут быть получены из некоторых других игровых ситуаций за одну "игру" или ход и в некоторых случаях, что представляет собой конфигурация, соответствующая выигрышу.
Это можно выразить на несколько более техническом языке, если называть игровую конфигурацию состоянием игры или просто состоянием и достижение некоторого состояния из некоторого другого состояния - переходом состояний. Пользуясь этой терминологией, правила абстрактной игры можно охарактеризовать как правила перехода состояний.
Bce интересные игры обладают допустимыми правилами перехода состояний. Эти правила позволяют игроку выбрать один из порой значительного числа ходов, когда наступает его очередь играть, за исключением, естественно, сравнительно редких ситуаций форсированного хода. В противном случае игра как таковая стала бы бессмысленной; весь ее ход и, следовательно, исход были бы предопределены даже еще до начала игры. Тем не менее может оказаться, что результат хотя и предопределен, но неизвестен участнику игры, и он хочет выяснить, каков он.
У человека может возникнуть желание узнать, сколько времени будет через 22 часа после 9 часов утра. Чтобы выяснить это, придется обратиться к упрощенному варианту математической игры, известной как "арифметика модулей". Один из способов введения основного правила этой игры сводится к утверждению, что "х по модулю z" представляет собой остаток деления х на z. В нашем случае игрок хотел бы знать, что будут показывать часы через 22 часа после 9, т. е. в 31 час. Его задача заключается в вычислении 31 по модулю 12. (Ответ-7 ч). Давайте, однако, действительно сделаем из этого игру. Расположим друг за другом 12 пустых пепельниц (рис. 2.1). Пусть у нас имеется также множество камешков. Начинает игрок с того, что складывает в кучку столько камешков, "сколько сейчас времени", т. е. в нашем случае 9. Затем он добавляет в эту кучку число камешков, соответствующее "числу часов, прошедших с данного момента", которое он имеет в виду, т. е. в нашем случае 22. Затем он вынимает один камешек из только что сложенной кучки и кладет его в первую пепельницу. Далее, вынув из кучки еще один камешек, он кладет его в следующую пепельницу и так далее вплоть до момента, когда он исчерпает всю кучку либо положит камешек в последнюю пепельницу.
Если в последнем случае в его кучке еще остаются камешки, то он повторяет всю описанную процедуру. В конечном счете исходная кучка будет исчерпана. В этой ситуации следует обратиться к последнему правилу: если какие-то пепельницы пусты, то ответ равен числу непустых пепельниц; если все пепельницы пусты, ответ 12 часов;
если же во всех пепельницах лежит по крайней мере по одному камешку, то игрок вынимает из каждой пепельницы по одному камешку, после чего снова обращается к последнему правилу.
Естественно, все это - просто многословное описание игры, состоящей в сложении двух чисел и последующем делении их суммы на 12 посредством последовательного вычитания. Правила этой игры не являются допустимыми; они не дают игроку возможности выбрать из ряда альтернатив переход из одного состояния игры в следующее. Они как раз, наоборот, точно предписывают, что должен сделать игрок для реализации перехода. Подобный набор правил, т. е. набор правил, точно указывающих игроку, каким образом следует вести себя при переходе из некоторой ситуации в следующую, называется эффективной процедурой.
Понятие эффективной процедуры, или "алгоритма", как ее также называют, в современной математике одно из важнейших. Дело не только в том, что значительная часть математики занимается отысканием эффективных процедур, обеспечивающих получение разнообразных полезных результатов, скажем, деления с выписыванием всех промежуточных шагов; существуют глубокие математические проблемы, связанные с фундаментальной природой самой математики, которые можно ставить и разрешать, сформулировав их как задачи, относящиеся к эффективным процедурам.
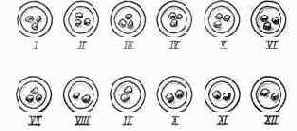
Рис. 2.1. Игра с пепельницами для определения времени.
Приведенное определение эффективной процедуры обманчиво просто. Обман заключен в словах "указывает игроку". Игрок, приступающий к решению задачи определения времени на основе только что сформулированных правил, должен сначала эти правила понять. Он должен знать, что значит сложить камешки в кучку, что такое пепельница, как определить, что пепельница пустая (допустим, что в ней лежат не камешки, а пепел) и т.
д. Другими словами, он должен быть в состоянии не только читать правила, но и интерпретировать их именно таким образом, который имел в виду я. И если правила должны "точно" указывать игроку, каким образом ему следует вести себя, то их следует формулировать на языке, позволяющем формировать точные высказывания.
Являются ли, например, эффективными процедурами рецепты поваренной книги? Они совершенно определенно предназначены для того, чтобы указывать человеку, что ему делать во время готовки в каждый следующий момент. Часто, однако, или даже как правило, они испещрены замечаниями типа "добавьте щепотку красного перца", "размешайте до нужного состояния" и "заправьте по вкусу". Разве не все согласятся с тем, что подобные указания далеки от точных? Тем не менее можно представить себе кулинарную академию, наделяющую своих студентов столь высоким кулинарным искусством и вкусом, что даже подобные указания, нечеткие для обычного человека, для них будут точными и однозначными. В таком случае подобные рецепты этой школы служат эффективными процедурами для ее выпускников. Но не обязательно для кого-нибудь еще.
Мое определение эффективной процедуры как некоторого набора правил, точно указывающих игроку, каким образом ему вести себя в каждый очередной момент, оказывается, таким образом, несовершенным по крайней мере в том отношении, что одного этого набора в чистом виде недостаточно. Зная набор правил, указывающих, скажем, как испечь пирог, мы не располагаем какими-либо абсолютными критериями, позволяющими установить, эффективна или нет эта процедура. Это затруднение снимается по крайней мере для кулинарных рецептов, если выполнены два условия: 1) существует некоторый язык, на котором можно сформулировать точные и однозначные правила приготовления пищи; 2) все люди абсолютно одинаковы во всем, что имеет хоть какое-либо отношение к кулинарии. Эти условия не независимы друг от друга, поскольку один из способов для всякого человека стать подобным кому бы то ни было еще заключается в том, что все будут идентично интерпретировать язык кулинарии.
С помощью этой системы кодирования можно транслитерировать [Прим. перев.: Транслитерация - передача текста, написанного с помощью одной алфавитной системы, средствами другой алфавитной системы] правила, заданные табл. 2.1, в правила, заданные табл. 2.3.
Каждое правило записывается на отдельной строке, а столбцы разделяются пустыми промежутками. Ничего не изменится, если исключить пустые промежутки и соединить строчки в одну длинную строку, состоящую из иксов, единиц и нулей. Эта строка будет представлять собой полное описание нашей суммирующей машины!
Мы сформировали систему записи, позволяющую описывать некоторую машину. Ее алфавит состоит из трех элементов: "X", "0" и "1". Строки, записанные с помощью этой нотации, естественно, не будут иметь смысла, пока мы не укажем, каким образом их следует
| X1X | X0X | Х111Х | X1X | X1X |
| X1X | XXX | X11X | X0X | X1X |
| X1X | X1X | X1X | X1X | X1X |
| X11X | X0X | X11X | X0X | X1X |
| X11X | XXX | X111Х | X0X | X1X |
| X11X | X1X | X11111X | X0X | X0X |
| X111X | X0X | Х111Х | X0X | X1X |
| X111X | XXX | X1111X | X0X | X0X |
| X111X | X1X | Х11111Х | X0X | X0X |
| X1111X | X0X | Х1111Х | X0X | X0X |
| X1111X | XXX | X1X | XXX | X0X |
| X1111X | X1X | X111111X | X1X | X1X |
| X11111X | X0X | Х11111Х | X0X | X0X |
| X11111X | XXX | X1X | XXX | X0X |
| X11111X | X1X | X1X | X1X | X1X |
| X111111X | X0X | XX | X0X | X0X |
| X111111X | XXX | XX | XXX | X0X |
| X111111X | X1X | Х111Х | X1X | X1X |
интерпретировать. Для этого было бы достаточно описать машину (или, еще лучше, построить ее), входами которой служили бы два информационных потока: один, содержащий должным образом закодированное описание нашей суммирующей машины, а другой - исходную конфигурацию иксов, нулей и единиц, с которой заданная указанным описанием суммирующая машина должна оперировать. Эти две так называемые цепочки символов, естественно, можно разместить на одной ленте. Когда мы будем иметь подобную машину, у нас появится право называть нашу систему нотации языком, поскольку имеется некоторая реализация его правил трансформации.
Одним из грандиознейших триумфов человеческого разума является доказательство в 1936 г. английским математиком Аланом М. Тьюрингом возможности построения подобной машины и, более того, указание способа ее построения1. На самом деле он доказал много больше, но об этом мы скажем позже. Я не имею возможности подробно описать машину, построенную в соответствии с принципами, сформулированными Тьюрингом, поэтому скажу о ней кратко.
Представим себе магнитофон типа использованного нами в суммирующей машине. В данном случае он также снабжен набором реле, позволяющих представлять состояния. Из-за того, что данная машина много сложнее нашей суммирующей машины, необходимо представлять много больше состояний и, следовательно, требуется больше реле (но это уже подробности). Лента, которая придается нашей новой машине, имеет следующую организацию (читаем справа налево):
участок, содержащий описание нашей суммирующей машины в предложенной системе нотации;
участок, содержащий данные, с которыми должна работать суммирующая машина, например, "X11X0X111Х";
участок для хранения текущего состояния суммирующей машины; участок (произвольной длины) "чистой" ленты, т. е. содержащий нули.
Информация, содержащаяся на ленте, имеет следующую структуру:
| чистая лента | текущее состояние | текущий символ | данные | описание машины |
Для того чтобы увидеть, как эта машина работает, необходимо задать какое-нибудь описание суммирующей машины, соответствующий набор данных и несколько условий. Например, начальным состоянием суммирующей машины всегда является 1; X, занимающий крайнее правое положение в наборе ее данных, представляет собой маркер, указывающий начало расположенных слева данных. Кроме того, требуется бумага для оперативных записей. Это все, чем располагает машина. Она перемещает ленту вперед и назад, считывает данные, делает отметки на своей ленте оперативной памяти и просматривает участок ленты, содержащий описание машины, отыскивая информацию, указывающую, что делать дальше.
Таким образом, в очень медленном темпе, шаг за шагом, и чрезвычайно точно имитируется работа нашей исходной суммирующей машины, т. е. машины, заданной новой машине через описание на ленте последней. Следовательно, машина олицетворяет правила, указывающие, каким образом интерпретируются цепочки иксов, единиц и нулей, предлагаемые ей нами.
Машину, которая перемещает ленту вперед и назад, считывая или изменяя метки на каждом такте в одной ячейке ленты и переходя из одного состояния в другое и так далее, теперь называют машиной Тьюринга. Описание такой машины является полным при условии, что для каждого ее допустимого состояния и для каждого символа, который может оказаться под ее считывающей головкой, это описание указывает, какой символ следует записать, в какое состояние должен произойти переход и в каком направлении машина должна передвинуть ленту. Можно в качестве особого условия оговорить, что всякая машина такого типа начинает свою работу из первого состояния (назовем его состоянием 1), причем лента расположена таким образом, что крайний правый записанный на ней символ располагается под головкой считывания (записи). Мы пользовались здесь языком, алфавит которого насчитывает три символа, с помощью их мы описывали нашу суммирующую машину. Если бы мы были щедрее, т. е. воспользовались алфавитом большего объема, наша машина могла бы быть проще - она имела бы меньше состояний. Правила же оказались бы более сложными. Существует, таким образом, множество возможных реализаций нашей суммирующей машины - по меньшей мере, по одной на каждый существенно новый алфавит, который мы могли бы выбрать. Минимальный объем алфавита, который можно использовать, равен двум - суммирующая машина типа нашей должна иметь большое число состояний, чтобы работать со столь ограниченным алфавитом. Минимальное число состояний, которое подобная суммирующая машина должна была бы иметь, равно двум, но такая машина должна оперировать большим алфавитом.
Существует важное различие между двумя рассматриваемыми машинами.
Наша суммирующая машина - специализированная, она может сложить два любых числа, но больше она ничего не может делать. Второй машине в качестве входной информации требуется закодированное описание некоторой машины и некоторое множество данных, с которым описанная указанным образом машина должна работать. В сущности, описание машины, задаваемое второй машине, представляет собой некоторую программу, преобразующую последнюю в ту машину, которую она должна имитировать. Естественно, возникает вопрос: "Какого рода машины можно имитировать подобным способом?"
Я показал, что понимается под формальным языком: некоторый алфавит; некоторое множество правил построения, определяющее длину построенных с помощью этого алфавита цепочек символов, которые являются правильными выражениями в данном языке; некоторое множество правил трансформации таких выражений. Я отмечал также возможность создания машин, являющихся реализацией таких правил трансформации и способных, следовательно, выполнять процедуры, представленные на соответствующих языках. Кроме того, мы рассмотрели некоторую машину, воспринимающую описания других машин и способную имитировать их поведение. Таким образом, мы усилили идею того, что понимается под имитацией В данном контексте. Обратите внимание, что я ни в какой связи не говорил о переводе с одного языка на другой. Наша имитирующая машина не начинает свою работу с перевода задаваемых нами правил трансформации, т. е. закодированного описания нашей суммирующей машины, на свой собственный или какой-то другой язык. Она обращается за консультацией (мы пользуемся словом "интерпретирует") к этому набору правил трансформации каждый раз, когда ей приходится определять, что должна делать имитируемая машина. Таким образом, на каждый шаг имитируемой машины должно приходиться множество шагов (машины) имитирующей.
Сейчас наша цель - создание надежной основы для нашего понятия эффективной процедуры. Мы стремимся к некоторому единственному языку, на котором можно выражать эффективные процедуры по крайней мере в том смысле, что с его помощью можно описывать все наши процедурные языки и снабжать, таким образом, процедуры однозначными интерпретациями.
Теперь можно убедиться в том, что правила трансформации языков можно реализовывать в виде машин. Следовательно, наша задача сводится к обоснованию возможности выбора единственного алфавита и языка, построенного на его основе, с помощью которого мы действительно сможем описывать все языки, привлекаемые нами для записи процедур.
Можно создать язык с алфавитом, состоящим всего лишь из двух символов ("0" и "1"), с помощью которого возможно описать любую машину Тьюринга. Теперь нам известно, что язык включает не только алфавит, подобно тому, как игра не исчерпывается теми принадлежностями, которые используются при ее реализации. Должны быть заданы также правила трансформации. В данном контексте я предполагаю, что правила трансформации языка, о котором идет речь, должны быть реализованы в виде некоторой машины Тьюринга, аналогичной рассмотренной нами имитирующей машине. Я утверждаю, следовательно, что существует некоторая машина Тьюринга, оперирующая с некоторой лентой, содержащей только единицы и нули, способная имитировать любую другую машину Тьюринга, какой бы она ни была. Эту так называемую универсальную машину, Тьюринга, как и вообще все машины Тьюринга, можно описать на языке множества пятерок уже знакомого нам вида: текущее состояние, считываемый символ, следующее состояние, записываемый символ, направление перемещения ленты. Эти пятерки, в свою очередь, можно записать на языке, который указанная машина Тьюринга по определению допускает. Следовательно, универсальная машина Тьюринга способна воспринимать некоторое свое описание и имитировать себя.
В действительности на основе одного и того же двухсимвольного алфавита можно построить много языков, т. е. много универсальных машин Тьюринга, реализующих правила трансформации цепочек, составленных из этих двух символов. Можно, естественно, и расширить этот алфавит и построить много универсальных машин Тьюринга, соответствующих каждому из таких расширений. Однако сейчас нас интересует собственно принцип, а именно: существует некоторая машина Тьюринга U (на самом деле, некоторый класс машин), обладающая состоящим из двух символов "0" и "1" алфавитом, которая при задании произвольной процедуры, записанной на произвольно точном и однозначном языке, и некоторой машины Тьюринга L, реализующей правила трансформации этого языка, может имитировать процесс исполнения этой процедуры машиной Тьюринга L.
Здесь мы перефразировали один из поистине замечательных результатов, опубликованных Тьюрингом в его блестящей работе 1936 г.
В математике имеется множество доказательств существования. Однако есть колоссальная разница между способностью доказать, что нечто существует, и способностью построить это нечто. Тьюринг доказал, что его универсальная машина существует, показав, каким образом она строится. Следует иметь в виду, что он создал эту монументальную работу в 1936 г. - примерно за десять лет до того, как были построены первые современные вычислительные машины. Они имеют мало общего с описанной машиной Тьюринга. Многие из них могут, например, оперировать одновременно целым рядом магнитных лент, и, что более существенно, большинство их имеют очень большую память. С функциональной точки зрения механизм памяти современной ЭВМ аналогичен набору реле, каждое из которых может быть либо включено (замкнуто), либо выключено (разомкнуто). Множество, состоящее из десяти таких реле, может принимать 1024 различных состояния. Нередко современные вычислительные машины среднего размера имеют более миллиона таких элементарных компонентов памяти и могут, следовательно, принимать 21000000 состояний. Это невообразимо большое число (Земля, например, весит меньше 21000 фунтов [Прим. перев.: фунт - английская мера массы (веса), 1 фунт эквивалентен 453,592 г.]). И все же, в принципе, любая современная вычислительная машина - это машина Тьюринга. Более того, любая современная вычислительная машина, за исключением очень небольшого числа специализированных машин, - это универсальная машина Тьюринга. И практически это означает, что любая современная вычислительная машина может, по крайней мере принципиально, имитировать любую другую современную вычислительную машину.
Имеется еще один пробел, который нам предстоит заполнить. Если даже допустить, что любая вычислительная машина в сущности может делать то же, что и любая другая вычислительная машина, то остается еще вопрос о том, что вообще могут делать вычислительные машины, т.
е. для осуществления каких процедур можно реализовать машины Тьюринга, и, следовательно, машины Тьюринга, поддающиеся имитации на универсальных машинах Тьюринга и, значит, поддающиеся имитации на современных вычислительных машинах. Тьюринг дал ответ и на этот вопрос: можно построить машину Тьюринга для реализации любого процесса, который было бы естественно назвать эффективной процедурой.
Этот тезис, называемый часто тезисом Черча (по имени логика Алонзо Черча), сформулировавшего его в ином, чем Тьюринг, контексте, не может быть доказан, поскольку содержит слово "естественно". Здесь у нас возникает в некотором смысле круг в доказательстве [Прим. перев.: Круг в доказательстве - логическая ошибка, состоящая в том, что доказываемый тезис обосновывается с использованием в данном доказательстве того же самого тезиса в качестве одного из оснований. Понятие круга в доказательстве - частный случай общего понятия порочного круга (или ложного круга), другим частным случаем которого является понятие круга в определении (когда, например, термин "А" определяется через термин "В", а "В" - через "А")]: любой процесс, поддающийся описанию в терминах машины Тьюринга, является эффективной процедурой и наоборот. Однако реальную интуитивную силу этой идее придает факт, что доказана эквивалентность четырех совершенно различных и независимо друг от друга полученных формулировок концепции "эффективной вычислимости" вычислимости в формализме Тьюринга и, следовательно, друг другу. Как замечает М. Минский, "доказательство эквивалентности двух или нескольких определений всегда производит неотразимый эффект, если эти определения отражают различные опыт и мотивацию"2 [Прим. перев.: В переводе цитируемой книги М. Минского на русский язык смысл этой фразы передан неверно]
Хотя мы и вынуждены полагаться на интуицию, давая определение, что "естественно" называть эффективной процедурой. Но можем точно и однозначно указывать, что именно эффективная процедура предписывает нам делать.
По крайней мере, в принципе, можно закодировать алфавит языка, на котором записывается процедура, с помощью всего лишь двух символов: "0" и "1". В таком случае правила, образующие процедуру, можно переписать в новой нотации. В конечном счете, некоторой универсальной машине Тьюринга, оперирующей на алфавите из нулей и единиц, можно задать правила трансформации языка процедуры в виде закодированных соответствующим образом пятерок. Заданная процедура предписывает нам делать то, что делает проинструктированная таким образом машина Тьюринга, имитируя "машину", описание которой мы ей задали. Если, в принципе, мы понимаем, как работает машина Тьюринга (а, как мы убедились, для достижения этого понимания требуется очень немного сведений), и располагаем некоторым описанием универсальной машины Тьюринга, о котором шла речь, то нам детально известно, что процедура предписывает нам делать.
Подобный способ узнавания очень несовершенен. Так, мы не считаем, что досконально знаем какой-то город, или хотя бы имеем представление о нем, опираясь только на факт наличия подробной карты этого города. В отличие от этого, если мы достаточно хорошо понимаем тот язык, на котором записывается некоторая процедура, чтобы иметь представление о его правилах трансформации, то, вероятно, мы понимаем, что предписывают нам делать правила, сформулированные на этом языке.
Однако эти возражения, справедливые сами по себе, не имеют отношения к существу дела. Тезис Тьюринга следующий: можно реализовать в виде некоторой машинной программы любую процедуру, которую "естественно" назвать эффективной. Таким образом, всякий раз, когда мы считаем, что понимаем некоторое явление в том смысле, что нам известны правила, определяющие его поведение, мы должны уметь воспроизвести свое понимание в виде некоторой программы вычислительной машины. Тьюринг доказал, что все вычислительные машины (за исключением небольшого числа вычислительных машин специальных типов, которые нас не интересуют) взаимно эквивалентны, т.
е. все они универсальны. Следовательно, всякий отказ правильно с технической точки зрения работающей вычислительной машины вести себя в точности так, как, по нашему мнению, мы ее запрограммировали, нельзя приписать какой-либо особенности используемой конкретной вычислительной машины. Причина ошибки должна заключаться: 1) в том, что (мы при записи правил поведения на формальном языке, используемом соответствующей вычислительной машиной, допустили небрежность; 2) в первоначальной экспликации [Прим. перев.: Экспликация (латинское explicatio - разъяснение, развертывание) - в математической логике способ развертывания какого-либо исходного понятия, которое еще не является вполне точным, в научно обоснованное понятие. В данном случае речь идет о замене интуитивного понятия (понимания!) строгим понятием (пониманием) ("экспликация" по Р. Карнапу)] (в любой форме) того, что мы имели в виду; 3) в том, что наше понимание имеет какие-то изъяны. Чаще всего дело заключается в последнем. Мы остановимся на этом несколько подробнее позже. Здесь же необходимо лишь заметить, что дефект нашего понимания может принимать следующие две формы.
Во-первых, хотя в целом наша теория может быть правильна, некоторые ее детали ошибочны. Мы можем, скажем, ошибаться, утверждая, что если то-то и то-то верно, то из этого следует то-то и то-то. Наше мышление, вероятно убаюканное чистой риторикой доводов, которые мы представляем себе сами, позволяет нам часто проходить мимо таких ошибок без малейших сомнений. Однако вычислительная машина в этом отношении совершенно неумолима. Она следует той логике, которую мы ей задали и которая может приводить к совершенно иным следствиям, чем процессы мышления, складывающиеся под влиянием стремлений достичь определенных результатов. В самом деле, одна из наиболее убедительных причин использования вычислительных машин - возможность обнаруживать слабые места в наших рассуждениях. В этом отношении вычислительные машины - безжалостные критики.
Во-вторых, ущербность нашего понимания может заключаться в том, что хотя понимаем мы правильно, но еще не в состоянии формализовать понятое.
Например, мы в состоянии с большой уверенностью предсказывать, что будет делать какое-нибудь животное при самых разнообразных обстоятельствах. Но наша способность предсказывать, возможно значительная и надежная, может основываться на интуитивных представлениях, которые мы просто не в состоянии адекватно эксплицировать. И все-таки мы иногда вынуждены так или иначе претворить наши идеи в формальный вид. Программа ЭВМ, основанная на построенной таким образом формальной системе, очевидно, будет вести себя плохо. В этом случае беда заключается не в том, что теория, воспроизводимая программой, содержит ошибки в деталях, а в том, что эта теория ошибочна в целом - в своих утверждениях о явлениях, которых она касается. Не всегда ясно, с каким именно дефектом вы имеете дело, когда запрограммированная вычислительная машина ведет себя неподобающим образом. Обычно наблюдается очень сильное стремление считать, что в целом с соответствующими теориями все в порядке, и в тех случаях, когда они работают плохо, должны существовать легко поддающиеся устранению ошибки в деталях. Нам придется позже подробнее остановиться на подобных проблемах.
Выше мы говорили об идее универсальности вычислительных машин. Теперь следует поставить вопрос: означает ли универсальность вычислительных машин, что они могут "делать все, что угодно". Этот вопрос на самом деле сводится к следующему: "Может ли все, что мы захотим сделать, быть описано в терминах эффективной процедуры?" Ответ на этот вопрос - "нет".
Во-первых, существует ряд вопросов, которые можно поставить и для которых можно доказать невозможность получения ответа с помощью какой бы то ни было эффективной процедуры. Например, мы захотим выяснить, остановится ли какая-то созданная нами машина (например, суммирующая), если она начала работу с некоторым определенным набором данных. Это удобно выяснить с помощью некоторой тестирующей машины, позволяющей для любой машины и любого предложенного последней набора данных устанавливать, остановится ли когда-нибудь эта машина, работая с заданным набором данных.
Но машину такого рода построить нельзя. Этот и множество подобных "неразрешимых" вопросов кладут некоторый предел тому, что вычислительные машины могут делать. Это, естественно, логическое ограничение, являющееся препятствием не только для вычислительных машин, но и для всякого вычисляющего - будь то человек или механическое устройство. Следует также отметить, что все множество неразрешимых проблем не так уж интересно с практической точки зрения; все вопросы такого рода чрезвычайно общи. Если мы имеем дело с каким-то определенным вычислительным процессом и хотим выяснить, закончится он когда-нибудь или нет, то обычно можно построить некоторую процедуру, позволяющую установить это. Но невозможно иметь некоторую машину или, что то же самое, эффективную процедуру, позволяющую отвечать на этот вопрос для любой процедуры в общем случае.
Во-вторых, некоторая эффективная процедура может в принципе позволить выполнить определенные вычисления, но для этого требуется так много времени, что процедура оказывается практически бесполезной. Например, обратимся к шахматам. Учитывая правило, согласно которому игра прерывается, если некоторая позиция на доске возникает три раза, можно определенно считать, что шахматы - конечная игра. Следовательно, в принципе возможно написать некоторую процедуру порождения списка всех партий, ход за ходом, которые вообще могут быть разыграны. Для завершения этого вычислительного процесса потребовалась бы, однако, вечность даже при использовании самых быстрых вычислительных машин, которые только можно себе вообразить. Это пример практически бесполезной процедуры. В самом деле, до сих пор мы обсуждали процедуры так, как будто время, необходимое для их реализации, т. е. для завершения соответствующей вычислительной задачи, несущественно. Подобный подход приемлем до тех пор, пока мы занимаемся абстрактными играми. В реальной жизни время имеет значение. Следует, в частности, иметь в виду, что, когда одна вычислительная машина имитирует другую, она должна на каждый такт работы имитируемой машины затратить множество сопряженных со значительными затратами времени тактов своей работы.
Если бы это было не так, мы бы отдали все свои силы созданию максимально дешевой универсальной машины Тьюринга, и, поскольку она могла бы имитировать любую более дорогую машину, она вскоре вытеснила бы с рынка все остальные вычислительные машины.
В-третьих, можно написать некоторую процедуру, реализуемую машиной Тьюринга, т. е. эффективную процедуру, но такую, в число правил которой не входит эффективное правило остановки. Процедура "начинайте с нуля, прибавьте единицу и, если сумма больше нуля, снова прибавьте единицу, и так далее" явно не остановится никогда. Можно было бы в этой процедуре вместо "если сумма больше нуля, снова прибавьте единицу" поставить "если сумма меньше нуля, остановитесь, в противном случае снова прибавьте единицу" и снабдить ее таким образом правилом остановки. Вычислительный процесс, выполняемый в соответствии с этой процедурой, никогда, однако, не вступит в контакт с этим правилом остановки, т. е. соответствующая машина Тьюринга никогда не примет состояния "сумма меньше нуля". Эта процедура в определенном смысле ущербна. Не всегда, очень мягко выражаясь, легко определить, свободна или нет от дефектов такого или подобного рода реальная процедура, написанная для реальных вычислительных машин.
И, наконец, мы подходим к наиболее неприятному моменту в вопросе, что вычислительные машины могут и не могут делать. Я снова и снова повторяю, что эффективная процедура - это некоторый набор правил, указывающих на точном и однозначном языке, что следует делать для перехода от одной ситуации к следующей. Я утверждаю, что некоторый язык точен и однозначен только в том случае, когда его алфавит и правила трансформации сами могут быть представлены в точных и однозначных терминах. И я повторяю тезис Чёрча (и Тьюринга): для любой такой экспликации какого бы то ни было языка существует некоторая машина Тьюринга, поддающаяся имитации с помощью универсальной машины Тьюринга. Я утверждаю далее, что, в сущности, любая современная вычислительная машина представляет собой универсальную машину Тьюринга.
Отложив все проблемы, связанные с неразрешимыми формально задачами, процедурами, не имеющими (конца и ущербными, мы неизбежно сталкиваемся с вопросом: сводимы ли все процессы принятия решений, используемые человеком, к эффективным процедурам и, следовательно, поддаются ли они машинной реализации?
Мы убедились в том, что сама идея эффективной процедуры неотъемлемо связана с идеей языка. Разве не странно, что я потратил столько времени на обсуждение языка безо всякого упоминания о значении? Причина, позволившая мне избегать конфронтации с понятием "значение", заключается в том, что обсуждались исключительно формальные языки или, как я говорил, абстрактные игры. Дело не в том, что значение вообще че играет никакой роли в подобных языковых играх.
Оно играет свою роль, но эта роль полностью погружена в правила трансформации языка. Напомним, что в алгебре можно преобразовать ас+bc в (а+b)с. Мы имеем право сказать, что эти два выражения означают одно и то же, или, выразив это по-другому, что использованное нами преобразование сохраняет "значение" исходного выражения. Если выразить это снова по-другому, то при подстановке вместо a, b и с чисел оба выражения дадут после выполнения указанных арифметических операций один и тот же результат. (Последнее, кстати, свойственно не всем алгебрам. Элементарная алгебра специально построена так, чтобы ее правила трансформации были совместимыми с правилами трансформации формального языка, называемого нами арифметикой.)
Действительно, особенностью формальных языков, их сущностью является то обстоятельство, что все их правила трансформации - сугубо синтаксические, т. е. описывают допустимые преобразования цепочек символов в данном языке, в том числе замену символов и введение новых символов (например, ")" и "(") независимо от того, какую интерпретацию подобные символы могут иметь вне рамок собственно языка. Можно, например, исписать алгебраическими преобразованиями целые страницы, слепо следуя алгебраическим правилам и не имея никакого понятия даже о том, что числа допустимо подставлять вместо маленьких букв и нельзя вместо скобок, т.
е. не давая используемым символам абсолютно никакой интерпретации.
Не так обстоит дело с естественным языком. Рассмотрим английское предложение: "I never met a man who is taller than John" (Я никогда не встречал мужчины, который был бы выше Джона). Его можно преобразовать в предложение "I never met a taller man than John" (Я никогда не встречал более высокого мужчины, чем Джон). Это преобразование совершенно очевидно сохраняет значение исходного предложения. Если применить это же правило трансформации к предложению "I never met a man who is taller than Maria" (Я никогда не встречал мужчины, который был бы выше Марии), то мы получим предложение "I never met a taller man than Maria" (Я никогда не встречал более высокого мужчины, чем Мария), и, следовательно, в этом случае правило неприменимо. Примененное нами правило не является чисто синтаксическим. Оно касается не только формы неинтерпретированных цепочек символов, но также и их значений.
Мы убедились в том, что на некотором определенном уровне рассмотрения нет существенной разницы между языком и машиной, олицетворяющей его правила трансформации. Мы отметили также, что, хотя законы, олицетворениями которых служат абстрактные машины, не обязательно должны быть логически совместны с законами физического мира, однако законы, реализуемые машинами, вступающими во взаимодействие с реальным миром, должны волей-неволей составлять подмножество законов, которым подчиняется физический мир.
Если мы хотим продолжать отождествление языков с машинами, даже обсуждая естественный язык, то необходимо признать, что какие бы машины не ставились в соответствие естественным языкам, они ближе к машинам, преобразующим и распределяющим энергию, чем к рассматриваемым нами абстрактным машинам, т. е. их законы должны принимать во внимание реальный мир. В самом деле, требования, предъявляемые к ним, являются более жесткими, чем те, которые предъявляются к "настоящим" машинам. И хотя законы настоящих машин - просто подмножества законов физики, законы некоторой естественноязыковой машины должны каким-то образом соответствовать внутренним реальностям личности каждого говорящего на данном языке, скрытым в ней или проявляющимся открыто в то время, когда он говорит.
В естественном языке в этой связи возникают трудности, поскольку мы должны знать, например, к каким "значениям" X и Y можно применять правило трансформации, обеспечивающее переход от фразы "I never met an X who is taller than Y" (Я никогда не встречал X, который был бы выше Y) к фразе "I never met a taller X than Y". (Я никогда не встречал более высокого X, чем Y). Это явно не такое правило, которое в равной степени может применяться к любым неинтерпретированным цепочкам символов.
Это затруднение даже серьезнее, чем может показаться с первого взгляда. Дело в том, что невозможно даже определить область применимости этого правила (а существует множество подобных) с помощью, скажем, перечней местоимений и существительных мужского и женского рода и мужских и женских имен, использование которых позволило бы соответствующим образом усовершенствовать правило.
Рассмотрим другую разновидность уже приводившегося примера - предложение "I never met a smarter man than George" (Я никогда не встречал более способного мужчины, чем Джордж). Представим себе детективный роман, в первой главе которого становится ясно, что разыскиваемым преступником является некто, выдающий себя за того, кем он не является. Опытный детектив разоблачает самозванца, скажем, в десятой главе. Одиннадцатая глава отводится объяснению читателю, который не смог прийти к выводам детектива на основании улик, разбросанных по всей книге, каким именно образом детективу удалось обнаружить виновного. Поэтому в одиннадцатой главе детектив объясняет, что он случайно услышал, (как на литературном вечере, посвященном творчеству английского писателя Джорджа Элиота, мистер Арботнот заметил: "Я никогда не встречал более способного мужчины, чем Джордж". Мистер Арботнот добился приглашения на вечер, убедив хозяйку дома в том, что он - специалист по английской литературе девятнадцатого века. Детектив подумал, что всякий, знающий хоть что-нибудь об английской литературе, должен знать, что Джордж Элиот - это псевдоним Мэри Энн Эванс - женщины.
Замечание мистера Арботнота было, следовательно, "грамматически неправильным" - так же, как математическое выражение х/у грамматически неправильно при у=0. Таким образом, мистер Арботнот не мог быть тем, за кого он себя выдавал.
Хорошая детективная история (может быть, нам следовало бы сказать "честная") - это такая, в которой читатель всю информацию, необходимую для выяснения истины, например "кто это сделал", получает до того, как выясняется, каким образом детектив пришел к своим заключениям. Вся суть детективного романа часто сводится к снятию неоднозначности того, что было сказано одним из героев где-то вначале. Сама возможность обнаружения неоднозначности, а следовательно, установление того, что ее необходимо устранить, и возможность раскрытия тайны зависят от знания читателем реального мира и от той особенности естественного языка, что его правила применяются к цепочкам символов, интерпретируемых в контексте реального мира. Историю подобного типа нельзя понять, обращаясь к чисто формальным средствам. Достаточно интересно, что первую главу этого детективного произведения невозможно перевести на другой язык, если переводчик не заметит и не поймет роковую ошибку мистера Арботнота и, таким образом, не поймет развязку, содержащуюся в последней главе.
Мы еще вернемся к роли контекста в понимании естественного языка как людьми, так и машинами. Пока мы заняты более ограниченной проблемой, по крайней мере более ограниченной в той постановке, которую мы рассматриваем здесь: сводимость процессов принятия решений у человека к эффективным процедурам, следовательно, к вычислимым процессам.
Естественно, существуют реализуемые человеком процессы принятия решений, которые можно ясно и однозначно описать даже на естественном языке. Мы описывали здесь игры, как на естественном языке, так и в терминах "конструкций" машин, которые, в свою очередь, описывались нами на естественном языке. В самом деле, мы не могли бы понять машину Тьюринга или эффективную процедуру, сформулированную в терминах машины Тьюринга, т.
е. как некоторую программу некоторой универсальной машины Тьюринга, не представляя себе, что значит, если одна ячейка ленты расположена рядом с другой, что значит считывать какой-то символ из некоторой ячейки ленты или записывать его на ней, что значит, если лента перемещается на одну ячейку вправо или влево, и т. п.
Особенно удивительно то, что мы невероятно мало должны знать для возможности обращаться в принципе ко всей математике. В обыденной жизни мы даем друг другу указания, т. е. описываем другим людям процедуры, которые, хотя, может быть, технически и неоднозначны (потенциально допускают различные интерпретации), во всех практических смыслах представляют собой эффективные процедуры. Они основываются на исключительно широко используемых словарях, элементы которых, появляясь в сугубо специфическом контексте, имеют эффективно-однозначные интерпретации. Во многих беседах на профессиональные и технические темы используются почти исключительно такие словари.
Задача преобразования подобных процедур в эффективные в техническом смысле процедуры - это по существу задача формализации базы знаний, лежащей в основе общепринятой интерпретации соответствующих словарей. Чем выше уровень стандартизации этих словарей и чем уже контекст их использования, тем выше вероятность решения задачи. Действительно, в конце концов, если каждый символ из некоторого множества символов обладает эффективной однозначной интерпретацией в некотором определенном контексте и если цепочки подобных символов преобразуются лишь согласно правилам, которые сами порождаются этим же контекстом, то в формальном смысле проблема интерпретации каждого символа вообще не возникает. Язык, ограниченный таким образом, - действительно формальный. Следовательно, его правила потенциально реализуемы посредством некоторой машины Тьюринга.
Однако остается еще много решений, принимаемых нами в повседневной жизни, для которых невозможно четко описать ни один процесс принятия решений. Как решить, какое слово нужно писать следующим? Возможно, наша неспособность в этом отношении всецело определяется тем, что мы до сих пор не добились адекватного понимания человеческого языка, сознания, мозга и символической логики.
В конце концов, поскольку все могут научиться имитировать универсальные машины Тьюринга, мы по определению сами есть универсальные машины Тьюринга. Это означает, что мы по крайней мере универсальные машины Тьюринга. (Даже некоторая реализованная физически машина Тьюринга - это не только машина Тьюринга; она может быть в то же время, например, настольной подставкой для книг или пресс-папье.)
Мы присоединяемся к Майклу Поляни, утверждающему, что мы знаем больше, чем можем выразить3. В результате мы попадаем в замкнутый круг. Наш вопрос имеет вид: "Что человек может сообщить вычислительным машинам?" Таким образом, под выражением "сообщить" мы понимаем "задавать эффективную процедуру". Теперь вопрос, который нас занимает, принимает вид: "Поддается ли все, что мы захотели бы сделать, описанию в виде эффективной процедуры?" Таким образом, утверждать, что существуют вещи, которые мы знаем, но не в состоянии выразить, не значит, отвечать на наш вопрос; это просто переориентация нашего внимания с понятия "сообщение", на котором до сих пор мы пытались сосредоточиться, на понятие "знание". Мы убедимся в том, что это очень уместный и имеющий решающее значение переход и проблема "что мы можем заставить сделать вычислительную машину" - это, в конечном счете, проблема "каким знанием мы можем снабдить вычислительную машину". Именно это и будет нашей основной темой в большинстве последующих частей книги. Вспомним, кстати, что мы уже затрагивали эту проблему; выше говорилось, что располагать картой города - не значит знать город. Так же умение изложить правила игры в шахматы не есть знание шахмат. Квалифицированный шахматист знает больше, чем может рассказать. Я не утверждаю сейчас (хотя и считаю, что это так), что мы никогда не найдем способ эксплицировать его шахматные знания целиком; я утверждаю лишь, что в этом случае мы имеем дело с примером знания, являющегося эффективным, несмотря на то, что в настоящее время оно не может быть сообщено.Если бы было верно, что шахматные знания квалифицированного шахматиста не поддаются полностью выражению, это значило бы, что никакая вычислительная машина никогда не сможет играть как квалифицированный шахматист. Отнюдь нет. Об этих проблемах говорится далее.
